Toán học là môn đòi hỏi rất cao trong quá trình học tập. Đây cũng được xem là bộ môn có khá nhiều ứng dụng trong cuộc sống. Muốn học được bộ môn này bạn phải học một quá trình từ những kiến thức cơ bản nhất đi lên thì việc học mới đem lại hiệu quả. Phần cơ bản nhất mà bất cứ ai khi học môn này cũng sẽ nhắc đến đầu tiên đó là số tự nhiên. Vậy theo bạn số tự nhiên là gì ? Bài viết sau đây sẽ đề cập đến số tự nhiên và tính chất của số tự nhiên.

Số tự nhiên
Trong Toán học, số tự nhiên được ký hiệu là N. N là một tập hơp bao gồm những con số lớn hơn hoặc bằng 0.
Các số 0, 1, 2, 3,… là số tự nhiên, và được ký hiệu như sau: N = {0;1;2;3;…}
Nhìn từ dãy ký hiệu ta có thể thấy được 0 là số tự nhiên nhỏ nhất và không tồn tại số tự nhiên lớn nhất. Ngoài ra khi ta bỏ số 0 trong dãy số tự nhiên sẽ được một tập hợp khác được ký hiệu là N*.

Một vài tính chất cơ bản của số tự nhiên:
- Trong một dãy số tự nhiên liên tiếp, các số sẽ có giá trị tăng dần.
- Số phía sau sẽ bé hơn số liền trước một đơn vị.
- Mỗi số tự nhiên chỉ có duy nhất một số đứng liền trước và một số đứng liền sau.
- Tổng số các số tự nhiên là vô số.

Số tự nhiên là nền tảng cơ bản để mở rộng ra các tính chất khác trong toán học. Các tính chất cơ bản được mở rộng ra từ số tự nhiên:
- Các phép tính cơ bản
- Quy tắc thực hiện các phép tính của số tự nhiên
- Tính chất của phép chia số tự nhiên

- Số tự nhiên nào chia hết cho 2, cho 5
- Số tự nhiên nào chia hết cho 3, cho 9
- Lũy thừa
- Ước và bội
- Số nguyên tố, hợp số. Phân tích một số ra thừa số
- Ước chung, ước chung lớn nhất
- Bội chung, bội chung nhỏ nhất

Các phép tính cơ bản
Số tự nhiên có 4 phép tính cơ bản đó là : cộng (+), trừ (-), nhân (*), chia (:).
Phép cộng: là gộp giá trị của 2 số tự nhiên lại thành 1 số tự nhiên, số tự nhiên này sẽ lớn hơn 2 số tự nhiên được cộng. Kết quả của phép cộng 2 số tự nhiên cho ra một số gọi lớn hơn được gọi là tổng. Kết quả của phép cộng hai số tự nhiên là tổng giá trị của hai số đó. Hai số tự nhiên được thực hiện trong phép cộng được gọi là số hạng.
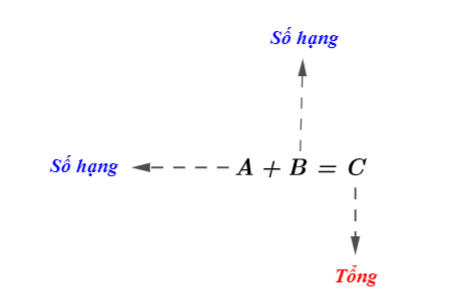
Ta có: số hạng + số hạng = tổng.
Ta có thể thực hiện phép cộng với 2, 3 , 4,… số tự nhiên giống nhau hoặc khác nhau.
Phép trừ: là phép tính ngược lại với phép cộng. Phép trừ sẽ lấy bớt ra giá trị của một số nào đó. Giá trị được lấy ra nhỏ hơn giá trị của số bị lấy bớt. Trong phép trừ sẽ có cách gọi các thành phần như sau: số bị trừ, số trừ, hiệu.

Ta có: số bị trừ – số trừ = hiệu
Tương tự như số trừ, ta cũng có thể trừ nhiều số tự nhiên.

Phép nhân: là phép tính đơn giản hóa của phép cộng nhiều số bằng nhau. Phép nhân sẽ cho ra kết quả từ việc nhóm các số tự nhiên khác nhau.

Ta có: thừa số * thừa số = tích
Ta có thể gọi bất kỳ 1 số trong 2 số của phép nhân là thừa số thứ nhất, số còn lại sẽ được gọi là thừa số thứ 2. Trong phép nhân có thể có nhiều thừa số.
Phép chia: là việc chia nhỏ một số tự nhiên. Trong phép chia, sẽ có cách gọi các thành phần của phép tính khác các phép cộng, trừ, nhân.
Ta có: số bị chia : số chia = thương
Phép chia cũng có thể gọi là phép tính ngược lại của phép nhân.

Quy tắc thực hiện các phép tính của số tự nhiên
Để việc tính toán được chính xác nhất, chúng ta phải nắm vững các quy tắc như sau:
Thứ tự thực hiện các phép tính với số tự nhiên:
- Đối với những biểu thức có phép trừ và phép cộng hoặc phép nhân và phép chia ta chỉ cần thực hiện các phép tính theo thứ tự từ trái qua phải.
- Những biểu thức không có bất kỳ dấu ngoặc nào ta sẽ thực hiện theo thứ tự như sau: tính các số chứa lũy thừa trước rồi đến các phép tính nhân chia, cưới cùng là phép cộng trừ. Các phép tính nhân chia hay là cộng trừ sẽ tính theo nguyên tắc từ trái qua phải.

Quy tắc dấu ngoặc trong các phép tính số tự nhiên:
- Khi bỏ dấu ngoặc của phép tính, ta hãy nhìn vào dấu trước dấu ngoặc. Nếu là dấu cộng, phép tính trong dấu ngoặc sẽ được giữ nguyên. Ngược lại, nếu trước dấu ngoặc là dấu trừ, ta phải thực hiện đổi dấu của các số trong dấu ngoặc. Cụ thể, dấu cộng (+) đổi thành dấu trừ (-) và dấu trừ (-) sẽ đổi thành dấu cộng (+).
- Đối với các biểu thức có nhiều loại dấu ngoặc, phải thực hiện phép tính trong dấu ngoặc tròn hay còn gọi là ngoặc đơn “( )” trước, rồi tới ngoặc vuông “[ ]” rồi tới ngoặc nhọn “{ }”.
Chia hết, chia có dư, tính chất của phép chia
Gọi a, b là 2 số tự nhiên cho trước, trong đó b khác 0.
Giả sử a = b*q + r (q, r là 2 số cho trước thỏa mãn biểu thức)
Có 2 trường hợp xảy ra:
- r = 0 => a = b*q: ta nói a chia hết cho b, ký hiệu: a ⋮ b
- trường hợp còn lại là r khác 0 sẽ nói a không chia hết cho b. Số a chia cho b được thương là q và r gọi là số dư. Ký hiệu tương tự như phép chia hết nhưng có dấu / ở giữa dấu ⋮

Tính chất của phép chia
- Nếu a chia hết cho n, b chia hết cho n thì hiệu của (a – b) chia hết cho n.
- Nếu a không chia hết cho n, b chia hết cho n thì tổng của (a + b) chia hết cho n.

Một vài dấu hiệu nhận biết chia hết:
- Các số có tận cùng là số chẵn (bao gồm các số 0, 2, 4, 6, 8) thì chia hết cho 2.
- Các số có tận cùng là 0 hoặc 5 thì chia hết cho 5.
- Tồng của các số có trong chữ số chia hết cho 9 thì số đó chia hết cho 9.
- Tồng của các số có trong chữ số chia hết cho 3 thì số đó chia hết cho 3.

Lũy thừa với số mũ tự nhiên
Ta có: an = a*a*a*…*a.
Công thức trên được gọi là lũy thừa bậc n của a. Lũy thừa bậc n của a là n thừa số a (n khác 0).
Trong công thức trên a được gọi là cơ số, n gọi là số mũ.
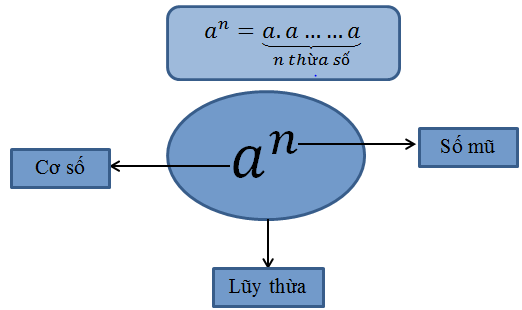
Ví dụ: 6^5: đọc là lũy thừa bậc 5 của 6, 5 gọi là số mũ, 6 gọi là cơ số
Trường hợp đặc biệt:
- n = 2: gọi là a bình phương (bình phương của a)
- n = 3: gọi là a lập phương (lập phương của a)
Ví dụ: 2^3: hai lập phương (lập phương của 2)
4^2: bốn bình phương (bình phương của 4)

Ước và bội
Cho hai số tự nhiên a và b. Giả sử a chia hết cho b.
a được gọi là bội của b
b được gọi là ước của a
Tập hợp những số là ước của a được ký hiệu là Ư(a)
Tập tập hợp những số là bội của a được ký hiệu là B(a)
Ví dụ: 6 chia hết cho 1, 2, 3 ta viết Ư(6) = {1; 2; 3}
Bội của 2 là 0, 2, 4,… ta viết B(2) = {0, 2, 4,…}

Số nguyên tố. Hợp số. Phân tích một số ra thừa số
Số nguyên tố là số tự nhiên lớn hơn 1 đồng thời thỏa điều kiện chỉ có hai ước là 1 và chính nó.
Ví dụ: 13 là số nguyên tố do 13 chỉ chia hết cho 1 và 13 hay nói cách khác 13 chỉ có ước là 1 và 13, Ư(13) = {1,13}.

Hợp số tương tự như số nguyên tố những nó có nhiều hơn 2 ước. Tức là ngoài 1 và chính nó thì hợp số còn có những ước khác.
Ví dụ: 12 là hợp số vì Ư(12) = {1,2,3,4,6}
Viết một số dưới dạng tích của các thừa số nguyên tố được gọi là phân tích một số ra thừa số nguyên tố.
Ví dụ: 26 = 2*13. 26 có hai thừa số nguyên tố là 2 và 13.
Lưu ý:
-
- Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố.
- Mỗi số nguyên tố chỉ có một dạng phân tích ra thừa số nguyên tố là chính số đó.
- Có thể viết gọn dạng phân tích một số ra thừa số nguyên tố bằng cách dùng lũy thừa.


Ước chung, ước chung lớn nhất
- Ước chung
Hai hay nhiều số có cùng ước thì các ước đó được gọi là ước chung.
Ký hiệu tập hợp ước chung là ƯC. Tập hợp các ước chung của 3 số a, b, c được ký hiệu là ƯC(a, b, c).
x ∈ ƯC(a, b, c) nếu a ⋮ x, b ⋮ x và c ⋮ x.
Ví dụ:
Ư(4) = {1; 2;4}; Ư(16) = {1; 2; 4; 8;16}.
Các ước 1, 2 vừa là ước của 4, vừa là ước của 16. Ta nói 1, 2 là ước chung của 4 và 16 và viết ƯC(4,16) = {1; 2}.
- Ước chung lớn nhất
Ước chung lớn nhất (ƯCLN) là số lớn nhất trong tập hợp ước chung của hai hay nhiều số.
Ký hiệu: ƯCLN(a,b): ký hiệu ước chung lớn nhất của a và b
Ví dụ:
ƯC(16, 20) = {1; 2; 4}. Nên ƯC(16, 20) = 4.

Bội chung, bội chung nhỏ nhất
- Bội chung
Bội chung là bội của hai hay nhiều số cùng lúc.
Bội chung có ký hiệu là BC
Tập hợp các bội chung của a, b được ký hiệu là BC(a, b).

Cách tìm bội chung:
Bước 1: Tìm hai tập hợp B(a) và B(b)
Bước 2: Từ hai tập hợp đã tìm, tìm ra các phần tử chung, tập hợp các phần tử này sẽ thuộc tập BC(a,b).
Ví dụ:
Ta có: B(4) = {0; 4; 8; 12; 16; 20; 24;…}
B(8) = {0; 8; 16; 24; 32; 40;…}
Hai tập hợp này có các phần tử chung là 0; 8; 16; 24;… Ta nói BC(4,8) = {0; 8; 16; 24;… } là tập hợp bội chung của 4 và 8.
- Bội chung nhỏ nhất
Số nhỏ nhất khác 0 trong các tập hợp bội chung của hai hay nhiều số gọi là bội chung nhỏ nhất.
Ký hiệu bội chung nhỏ nhất của hai số a và b là BCNN(a; b)
Ví dụ:
Ta có: B(5) = {0; 5; 10; 15; 20; 25; 30;…}
B(10) = {0; 10; 20; 30; 40; 50; 60;… }
BC(5; 10) ={0; 10; 20; 30; 40;…}
BCNN(5; 10) = 10

Lưu ý:
- Tất cả các bội chung của a và b đều là bội của BCNN(a, b).
- Mọi số tự nhiên đều là bội của 1.
- Với mọi số tự nhiên a và b (khác 0) ta có: BCNN(a, 1) = a; BCNN(a, b, 1) = (a, b).
Việc học tập luôn đòi hỏi phải đi từ cơ bản đến nâng cao. Mặc dù số tự nhiên nhìn thoáng qua rất đơn giản dễ hiểu không có gì phức tạp nhưng nếu ta không hiểu gì về số tự nhiên thì việc học sau này sẽ có nhiều khó khăn. Chính lẽ đó, muốn học tốt trước tiên phải trả lời được câu hỏi số tự nhiên là gì ? Bài viết bên trên đã cung cấp các kiến thức về số tự nhiên; tính chất của số tự nhiên. Mong rằng bạn đọc sẽ áp dụng được những kiến thức này vào bộ môn Toán học cũng như áp dụng vào việc tính toán trong đời sống.




























Ý kiến bạn đọc (0)